Folytatjuk a perspektíváról szóló sorozatunkat a kétpontos perspektívával. Kérem csatolják be biztonsági öveiket: Egy kis agymunka következik…
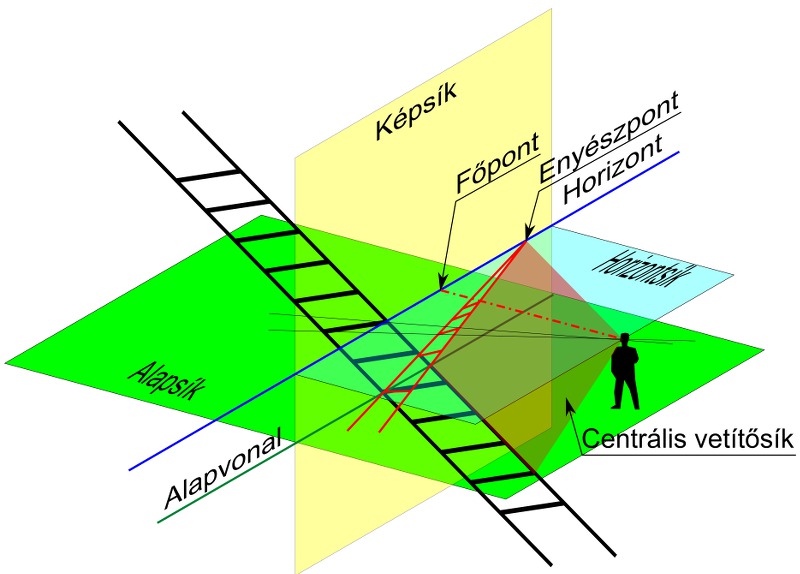
A kétpontos perspektíva geometriai viszonyai az ábrán láthatók. Az alapsíkon állunk, szemünk az a pont, melyre minden irányból befutnak a fénysugarak, a kép a képsíkon képződik.
Szemünk magasságában húzódik az alapsíkkal párhuzamos horizontsík, mely a képsíkot a horizontvonalban metszi.
Az ábra az alapsíkon átvonuló sínpár és a talpfák perspektív képének keletkezését szemlélteti. A kocka perspektívája szerkesztését nagyon egyszerű megérteni, ha meggondoljuk, hogy a képsíkot átható egyenesek döféspontja mind eredeti nagyságban látszik. Nincs tehát más dolgunk, mint megkeresni a kocka azon pontjait, melyek metszik az alapvonalat.
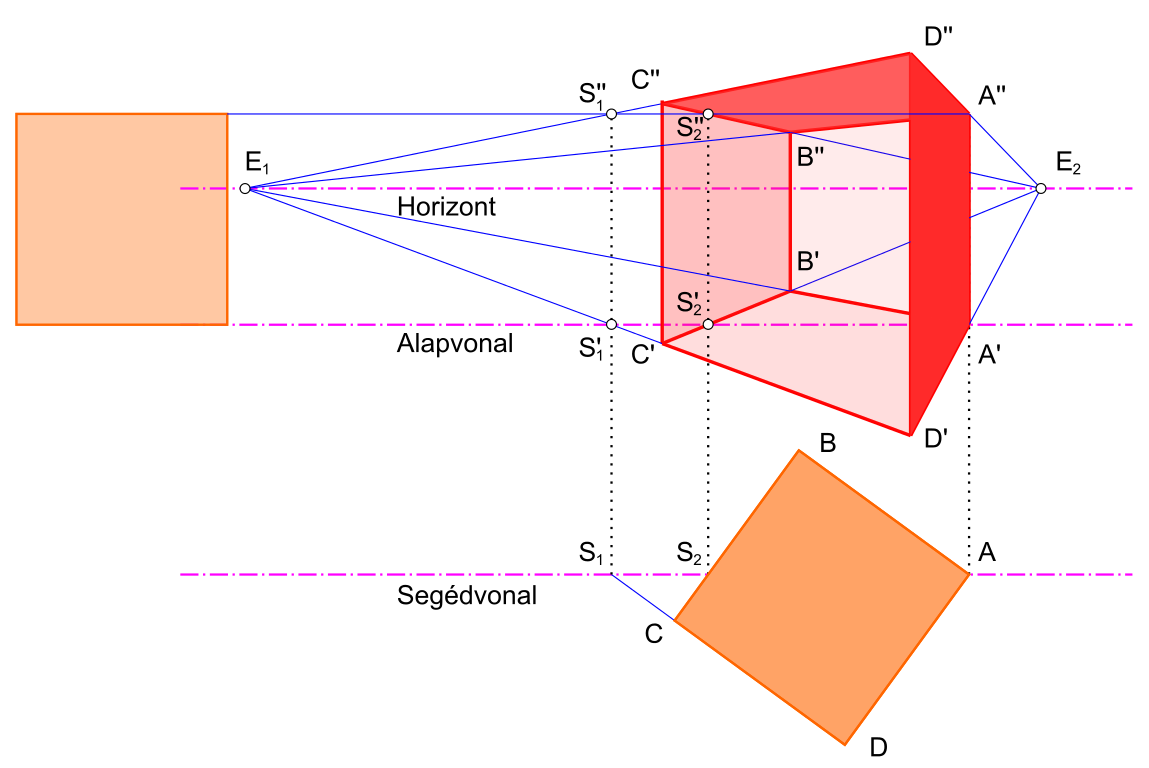
Az ábrán a kiinduló adatok: a horizontvonal, az alapvonal és a segédvonal.
Ez utóbbi tulajdonképpen az alapvonallal azonos, csak azért húztuk lejjebb, hogy a szerkesztővonalak ne kuszálódjanak össze, ha a szerkesztést csak az alapvonal segítségével hajtjuk végre.
Fel kell még vennünk a kocka két (nem összetartozó) képét. A felsőt az alapvonalra állítjuk, az alsót (a felülnézetet) tetszés szerinti szöggel elforgatjuk. A felsőre sincs igazán szükség, elegendő az élhosszúságával párhuzamosat rajzolni az alapvonallal.
Fel kell még vennünk a horizontvonalon az E1 és E2 enyészpontot.
A képsíkon három pontot tudunk kijelölni: az A pont éppen az alapvonalon van, ezért egyszerűen felvetítjük, így megkapjuk a perspektíva A’ pontját.
A kocka élhosszúságával feljebb helyezkedik el az A” pont. Az A’A” él eredeti nagyságban látszik, mert teljes egészében illeszkedik a képsíkra.
Az E2 enyészpontot az A’-vel és A”-vel összekötve megkapjuk az A’D’ és A”D” élek irányát.
Ha a felülnézeten meghosszabbítjuk a CD oldalt, az kimetszi a segédvonalon azt az S1 pontot, mely a CD sík és a segédvonal metszésvonalának képe. Mivel ez is a képsíkon van, a perspektívában adódik a képe az S1′ és S1” pont formájában. Ha e két pontot összekötjük az E1 enyészponttal, megkapjuk a C’D’ és C”D” oldalak egyenesét. A C’D’ és A’D’ egyenes metszéspontja kiadja a D’ pont helyét, hasonlóan meghatározhatjuk a D” pontot is.
A felülnézetből látszik, hogy a CB sík S2-ben metszi az alapvonalat és így a képsíkot is.
Ennek segítségével felvetíthetjük az előzőekhez hasonlóan az S2′ és S2” pontokat is, melyek segítségével most már az összes csúcspont felrajzolható, és így a kocka perspektivikus képe is elkészült.
(Az ábrán a kocka mellső lapját eltávolítottuk, hogy a takart csúcspontok szerkesztése is láthatóvá váljék.)