Van az Inkscape eszközei között egy rejtélyes darab, melynek neve 3D téglatest. Térbeli testek vagy felületek az Inkscape-ben? Nem, persze, hogy nem, hiszen a program egy síkbeli vektorgrafikus szerkesztő. Vannak persze háromdimenziós geometriát létehozó szoftverek, CAD programok (pl. a CATIA, az Inventor vagy a szabad forráskódú és ingyenes FreeCAD) és 3D modellező-animációs programok (pl. Blender), melyek valóban térbeli objektumokat hoznak létre, de az Inkscape nem ilyen, ezzel „csak” a térbeli objektumok valósághű képét lehet megrajzolni. A 3D téglatest ezt a munkát segíti, de nem végzi el helyettünk.

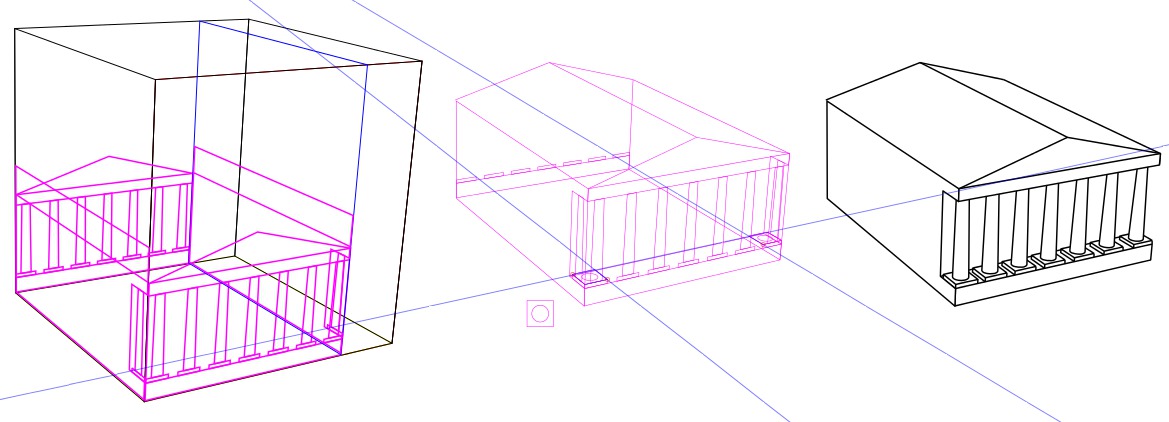
A 3D téglatest eszköz a fentiek értelmében nem rajzol térbeli testet, csak segítséget nyújt perspektivikus, távlati képük megrajzoláshoz. Alkalmazásához célszerű a nyomtatható lap keretét megjeleníteni, majd ezután hívni az eszközt és egérhúzással felvázolni egy téglatestet a lap területén belül. (A kereten kívül néha teljesen torz alakzatok is születhetnek.) Az eredmény az ábrához hasonló lesz.

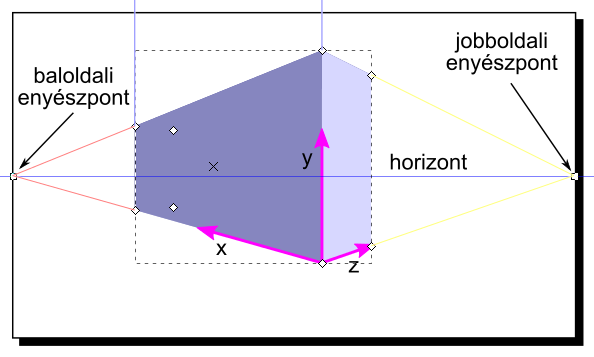
A téglatest csúcspontjai (a takarásban lévők is) csúcsaikra állított négyszögekkel jelennek meg, ezek vonszolásával a téglatest méretei változtathatók. Perspektívában a téglatest oldalainak képe (bár a valóságban párhuzamosak) egy-egy pontban, az enyészpontban találkoznak. Esetünkben az enyészpontok a keret oldalainak felezőpontjait összekötő egyenesen, a horizontvonalon helyezkednek el. Az ábrán látható esetben az X és Z irányú egyenesek összetartanak, az Y irányú oldalak azonban párhuzamosak maradnak.

Perspektíva

Ezt a fajta ábrázolást két enyészpontos perspektívának nevezik. A téglatest méretei és helyzete a fogópontokkal változtatható.

Ha az első 3D téglatest már a képernyőn van, minden további ugyanazokat a paramétereket és enyészpontokat használja, mint amit elsőre felrajzoltunk.

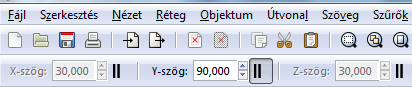
Eddig nem említettem, de az eszköz hívásával egyidejűleg megjelenik a képen látható eszközvezérlő sáv, melyen a perspektíva tengelyeinek szögét lehet beállítani. A fenti téglatestnek megfelelő (alapértelmezett) beállításnak az Y tengely 90°-os szöge és a függőleges élek párhuzamos volta felel meg, az X és Z tengelynél a szög értéke ki van kapcsolva, mert ott enyészpontok vannak. A szögek értékének, valamint az enyészpontok számának és helyének megválasztásával változatos távlati képeket állíthatunk be.

A legáltalánosabb a hárompontos perspektíva, ahol három enyészpont van a képen, kettő általában a horizontvonalon, egy pedig magasan felettünk vagy mélyen alattunk. Ebben az esetben mindhárom tengely szöge ki van kapcsolva. A hárompontos perspektívát ritkán kell használni, ahogy ez az Empire State Building fényképén is látható: az épület minden irányban kiterjedő hatalmas arányait hangsúlyozzák vele.

A kétpontos perspektíva az első példában már szerepelt, a legtöbb esetben kielégítő távlati képet ad, ha az ábrázolt tárgyak magassága sokkal kisebb a szélességi és hosszméreteiknél. Az Egyesült Államok arlingtoni temetőjének fényképe példázza, hogy a messze futó sírkő-sor méretei mellett az egyes kövek magassága elhanyagolható.

Sok esetben az egypontos perspektíva is megfelel, ennek legnagyobb előnye, hogy a rajz pontos szerkesztése egyszerűbb, mint a többi perspektíváké. Itt két tengely (az ábrán az Y és Z) irányában a téglatest élei párhuzamosak, X irányban egyetlen enyészpontban találkoznak. Amikor az enyészpont középen helyezkedik el, az elrendezést homlokzat perspektívának hívják és gyakran alkalmazták a reneszánsz művészek, mint Sandro Botticelli Angyali üdvözlet képe is példázza.

Ha mindhárom irányban párhuzamosak az élek, az ábrázolást axonometriának hívják. Ezt a fajta ábrázolást ma főleg a műszaki feladatoknál használják, mert egyszerűen szerkeszthető, és ha bizonyos szabályokat betartanak, az eredményül kapott kép is szemléletes marad.

Axonometria

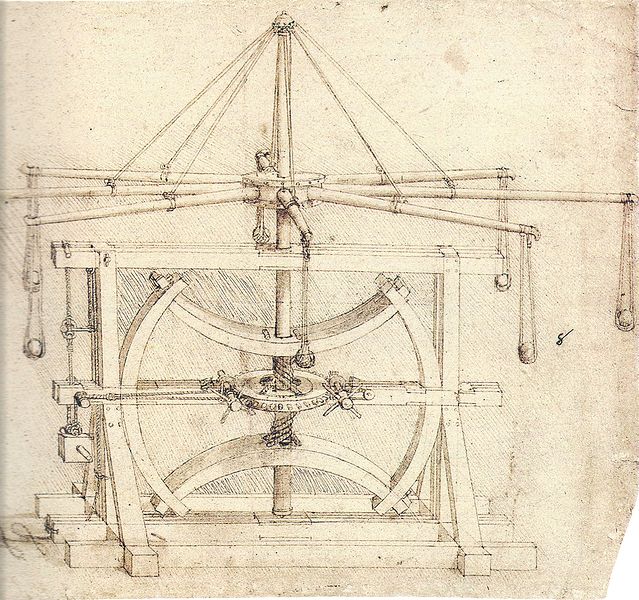
Mielőtt a reneszánsz művészek és tudósok felfedezték a perspektívát, a tér ábrázolására az axonometriát használták, a keleti (kínai, japán) művészeteknél ez a gyakorlat később is megmaradt. Ha az axonometria tengelyeinek szögét bizonyos szabályok szerint vesszük fel, pontos, mérethelyes merőleges vetületeket készíthetünk, anélkül, hogy több összetartozó képből kellene fáradságos munkával megszerkesztenünk. Lejjebb Leonardo da Vinci hadigépe, egy japán XVIII. századi rajz és Ottó német-római császár román kori képe látható, mindegyiknél axonometriával találkozunk.

Leonardo da Vinci hadigépe.

Japán rajz a XVIII. századból.

Ottó német-római császár román kori képe.

Három ilyen különleges axonometria van:

1. Az izometrikus axonometria szögei: X = 210°, Y = 90°, Z = 330°. Mindegyik tengelyre azonos léptékben lehet felmérni a méreteket, ezeken a rövidülés azonos, ezért nagyon egyszerű a használata, de hátránya, hogy kevéssé érezzük valósághűnek a képet. Természetesen minden más irányban a rövidülések különbözőek, így például a kocka lapjára rajzolt kör ellipszissé torzul. Leginkább különleges műszaki alkalmazásoknál használják (pl. cső műhelyrajz egy vetületben való ábrázolásához).
   
   
2. Cavalier-axonometria. Szögei: X = 225°, Y = 90°, Z = 0°. Az Y és a Z tengelyre eredeti nagyságában, az X tengelyre pedig fele akkora nagyságban kell felmérni a távolságokat. Az YZ homloklapon egyik irányban sincs rövidülés, az ide rajzolt kör változatlanul kör marad, de természetesen az XY és XZ síkokon a itt is ellipszissé torzul.
   
   
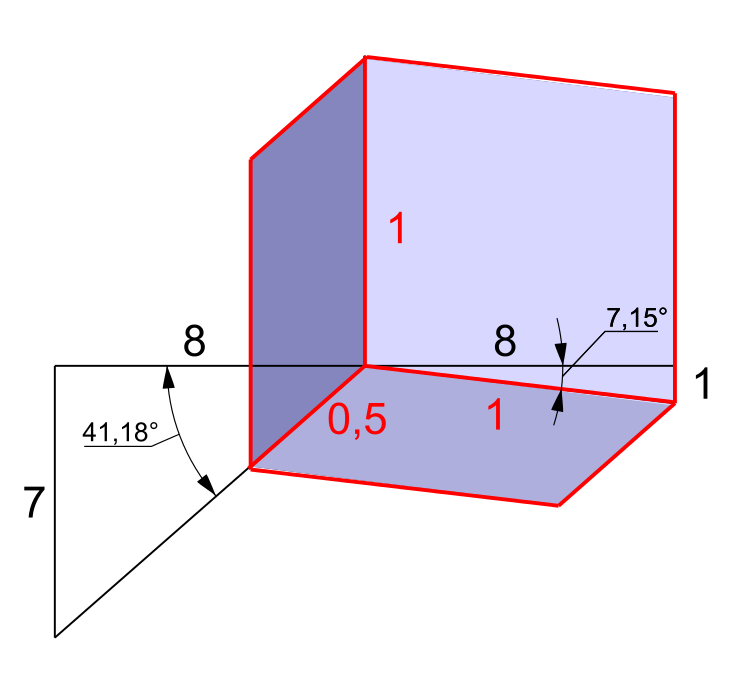
3. Dimetrikus axonometria. Az ábrán látható a tengelyek irányának felvétele. A fekete számok azt jelzik, hogy az adott irányba hány hosszegységet kell felmérni megrajzolásukhoz. Emellett látszik az X és a Z tengely szöge is. Ha a 3D téglatesttel kívánjuk felrajzolni, a tengelyek szögei: X = 221,8°, Y = 90°, Z = 352,85°. Az Y és Z tengelyekre itt is az eredeti nagyságot, az X tengelyre az eredeti méretnek felét kell felmérni. Ez az axonometria szebb képet eredményez, mint a Cavalier-axonometria, és alig valamivel bonyolultabb a szerkesztése.

Mit tud ezen kívül a 3D téglatest? Hát nem sokat. Én a magam részéről nem is használom, helyette egyszerűbb, ha a hagyományos Inkscape technikát és a fejünkben lévő tudást alkalmazzuk (erre egyébként is szükség van). A 3D téglatest ugyanis a legfontosabbról semmit nem mond: hogyan kell kezelni a méreteket a perspektívában.

(A cikk folytatása következik…)